Round Robin Calculator.

Round Robin bet is a combination bet, which is combined of several simple bets. Round Robin by M bets of N bets is set of all possible parlays of M bets, which are selected from N bets full set. For example Round Robin by 2 of 6 is a set of 21 parlays, each containing 2 bets. They are selected in various combinations from all 6 bets. The number of parlays is , which is a number combinations by 2 of 6. Each parlay is assigned by equal sum, so that total sum is equal of total round robin bet sum. In our sample if round robin bet sum is $21, then each parlay is $1 bet. After all games are over, results of all parlay bet are totaled.

M and N parameter are selected in upper left part of calculator window. In order to rebuild page you need click Change Table button.

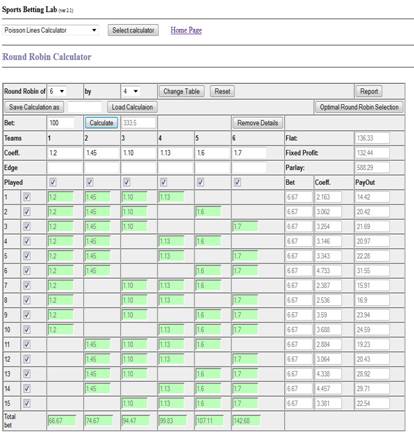
Lines (coefficients) for simple original bets can be entered manually, each entered in corresponding text box under bet number. But they can be entered all at once if they are entered in large text area under calculator window. To get these lines you click Read Coefficients button. Coefficients are to be entered in d.dd format, for example, 1.22, 4.53, 12.10 and so on. Thus you need to enter two digits after point delimiter. You can get the odds from bookmaker page by copy-paste operation. All extra text will be ignored. The coefficients will be placed in bet boxes in order which they are located in the whole large text area. Extra coefficients will be ignored.

The bets won are marked by checkboxes under corresponding coefficients. To get payout value you need to click PayOut button. There is a possibility to calculate partial round robin, unchecking checkboxes from unneeded parlays, in the left part of the table.

If you need not detailed information for each parley then you could remove it by clicking button Remove Details.

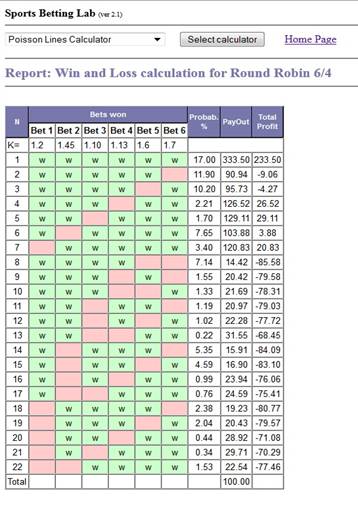
You can get payout for various combinations of won and lost bets by checking or unchecking checkboxes under games coefficients and then clicking PayOut button. Another way to get similar information is to use Report button. When pressing Report button you get new window where various combinations of won/lost bets are supplied with corresponding payouts.

Another unique feature or the calculator is Optimal Round Robin Selection button. If you press the button maximum and minimal winnings are calculated for a given bets set when using various round robin cases and various numbers of lost bets. Then you can select optimal, in some sense, round robin parameters depending on bets coefficients. Various cases of round robin bet give us a set of facilities from ordinary bets up to full parlay. The more length has parlay in round robin, the more are you potential winning in favorite case, but the more you lose in total if some bets are lost. For example, you can calculate round robin so, that losing one bet does not lead to loosing round robin as a whole.

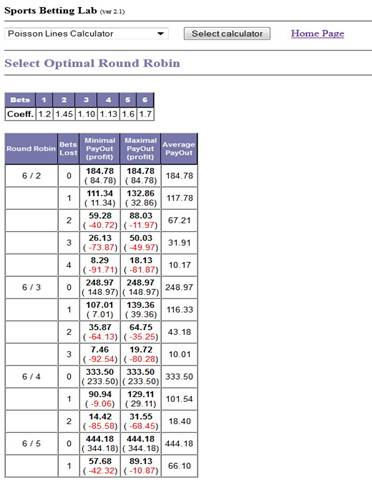
In this sample round robin we see that in case you lose one bet round robin 6/2 and round robin 6/3 give approximately the same winning. But if you lose two bets, then round robin 6/3 is a bit more risky than round robin 6/2. From other point of view if all bets win, then round robin 6/3 is much better than 6/2.

All data entered in the form, including round robin parameters, coefficients, checkboxes for bets that win, can be saved in a file. Later we can load this data set and continue round robin analysis.

Consecutive Round Robin.

It is a kind of my own ‘invention’. Everybody knows that parlay can be rolled in time, that is can be ‘emulated’ by ordinary consecutive bets, each made one after another. This kind of parlay can be titled as ‘parlay in time’. It has several advantages upon traditional (simultaneous) parlay and is used by some bettors as a kind of interesting financial strategy. But there is another combination bet besides parlay – it is round robin. Here we develop new version of round robin, called consecutive round robin, which is related to traditional round robin the same way as consecutive parlay (parlay in time) is related to ordinary parlay.

The same way as in parlay in time, bets in consecutive round robin are not made in one moment, but one after another. All advantages of parlay in time are enabled in consecutive round robin. Among the advantages – possibility to select bets not restricted by bookmaker rules for round robins, possibility to wait ‘good’ bet if you have not any at the moment.

To execute consecutive round robin we need to develop its plan. For parlay in time we have very simple plan, it is even need not to be formulated. But in consecutive round robin we can not work without plan, and the plan can be produced only using a program.

Let us suppose that we need to execute consecutive round robin by 3 of 5. Below you see a picture, which represents calculations for ordinary round robin and was produced using our Round Robin Calculator. In case or ordinary, nonconsecutive round robin we know all lines (coefficients) in advance and the picture gives us not only round robin plan, but also demonstrates financial results.

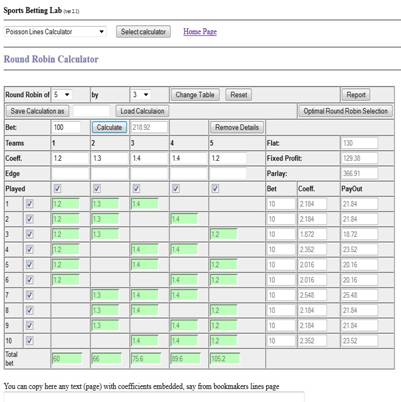
Now let us suppose that we execute the round robin consecutively. Firstly we have only one bet and we make it. What is to be its size, taking into account that full round robin bet size is to be $100. Looking at the round robin plan we see that first step consists of a start of 6 parlays each $10 in size. So, when emulating the round robin we need to finance our first bet by $60 = $10 * 6. This sum we can see at the bottom row having title Total Bet, in the first column. This row is specially added to the calculator for planning consecutive round robin.

Let us suppose that first bet won. For second bet we have three parlays continuing and three parlays starting. Because three parlay continue and the first bet has coefficient 1.2 and won, then the sum of these three bets is $10*1.2 = $12 each, or $36 in total. Also we start three new parlays each $10 in size. So, we have calculated for second bet the value equal $36+$30=$66.

Let us suppose then that the second bet also won. For next, third bet we have according to our plan:

We continue parlay N1 – its sum is now $10*1.2*1.3 = $15.6

We continue parlays N4 and N5 – they are equal (till the moment), each having $10*1.2 = $12, $24 in total for two parlays.

We continue parlays N7 and N7 – they are equal (till the moment), each having $10*1.3 = $13, $26 in total for two parlays.

We start parlay N10 – its initial sum is $10.

So, we have for the third bet $15.6+$24+$26+$10 = $75.6. This value we see in 3^rd column of the last row in calculator table.

Further we could continue the same way and get bet sizes form all next consecutive bets. You can see them in last calculator row: 4^th bet = $89.6, 5^th bet = $105.2

By defining bets sums according this scheme we will get exactly the same financial result as if we have made ordinary round robin, which is made at one moment.

In case when all bets won. It is the idea for building the consecutive round robin scheme.

We have considered in details the case when all bets won. But round robin is usually used instead of parlay in order to insure bettor in case of one or two bets possibly lose. In this case round robin does not lose the whole sum as in parlay. But round robin has a lower total coefficient for case when all bets won.

Let us describe the similar consecutive round robin scheme when one bet loses, in the middle of the course.

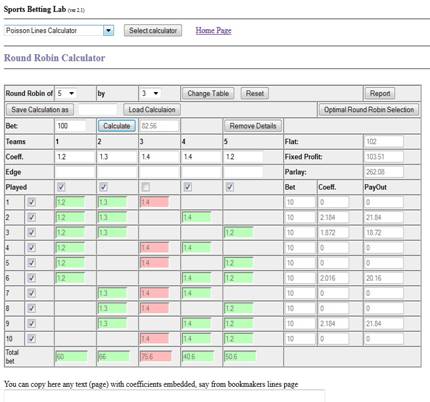
As we see first three bets we make using the same scheme as in previous example. But in this case third bet loses. It means that we decrease of the following bets by the sum of parlays that were stopped. After third bet was lost we have parlays N1, N4, N5, N7, N8, N10 stopped. But parlay N1 is already over and does not influence next bets.

Thus consider how these parlays influence next bet sum. The only active parlays, where bet N4 is contained in, are parlays N2,N6,N9. They have current sizes:

Parlay N2: $10*1.2*1.3 = $15.6.

Parlay N6: $10*1.2 = $12.

Parlay N9: $10*1.3 = $13.

Thus we get $40.6 for 4^th bet when emulating consecutive round robin. The value we can see in the 4^th column of the last row (do no forget to mark 3^rd bet as lost in the calculator table). The financial result of this round robin emulation is exactly the same if when we make it in one moment.

When emulating round robin we can run against the situation when bet loses. What to do then. We can continue realizing the initial scheme in order to have minimal loss which is defined by calculation of financial result when losing one bet. In our previous example when we lose one bet and no more, we get 82.56% of initial bet sum invested. Thus we lose only 17% of the bet sum.

The second way is to increase sums for remaining parlays – that is, to use slight progression strategy, hoping we will not lose no more (especially when coefficients are low). For example, in order to try to return our money back we need to increase each bet in scheme by 100/82.56 = 1.2 times. If we get first bet in our scheme lost then to get money back we could try to increase each next bet by 100/92.68 = 1.07 times. If despite one bet loss we are aiming at getting the same profit as before we need to increase all next 4 bets by 2.4 times. In this case total round robin size will be increased to $60+$4*24= $156., a bit more than in 1.5 times.

The third way: stop round robin and start new one. In our example we go out the round robin having sum equal $10*1.2*1.3+$10*1.2*1.3+1.2*$10+1.3*$10 = $31.2+$13+$12 = $56.2. Thus we leave our round robin when losing less than 50% of initial bet size. If we lose at the first bet of round robin and go out it - we lose 60% of initial bet size.

Mathematically neither parlay nor round robin has neither advantages, nor drawbacks in comparison with single ordinary bets when our edge is equal to zero. Thus I described the consecutive round robin only in order to fill the gap in combination bets set. Nevertheless there is a series of nonmathematical advantages that allow including this consecutive round robin it bettor toolbox. Taking into account that we have software that can build consecutive round robin plans.

In conclusion I will emphasize once more that no manipulation with bets sizes, which can be seen in parlays or round robin, are they made consecutively or at one moment, cannot increase bettor edge for a given bet(s). They only can make some insurance when risking money, find compromise between bankroll growth and risk of losing it. It is valid only when a bettor has an edge- that is has capability to select sets at relatively (reality) high coefficients.