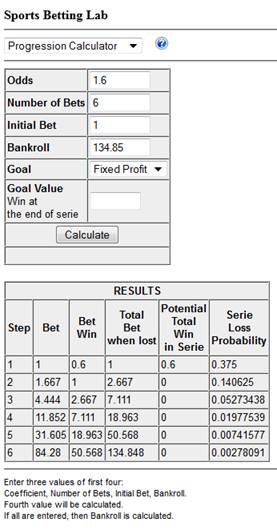
Progression
Calculator.
The calculator allows determining the
following:
1. Bankroll size, which is required for
progression system with a given coefficient in order to insure feasibility of a
given progression size. The goal of the progression can be achieving fixed
profit (if zero, then no losing), achieving fixed ROI (return on investment).
2. For each progression step: current
bet sum, potential winning sum, losing probability. This probability is not the
probability of losing current bet, but probability of losing a series of bets
from the beginning till current bet including it. Probability of losing current
bet can be estimated using bet’s line.
The formula for bankroll size in
order to have a fixed profit at the end: ![]() ,
,
Here:
S – bankroll size required
B0 – initial bet
k – bet coefficient
N – number of bets in progression series
G – fixed winning required (at first bet
it is equal by initial bet sum). If G = 0, then goal is not to lose.
Solving this formula
in relation to k, N, è
B0 you can calculate any other progression
parameters using three other defined. For example, using initial bet size,
current bankroll and coefficient you can calculate series size, which can be
achieved even when you lose every bet in it.
The formula
for bankroll size in order to have fixed ROI(Return On Investment) at the end
of series : ![]() ,
,
Here:
S – bankroll size required
B0 – initial bet
k – bet coefficient
N – number of bets in progression series
f – ROI required (at first bet it is
equal by initial bet sum and coefficient).
If f = 0, then goal is not to lose.
Solving this formula
in relation to k, N, è
B0 you can calculate any other progression
parameters using three other defined. For example, using initial bet size,
current bankroll and coefficient you can calculate series size, which can be
achieved even when you lose every bet in it.
Below we show calculation of a progression system
which has coefficient equal to 1.5 in order not to lose.